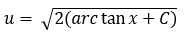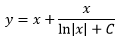Solving Physics Problems (Part 2)

Continuing with solving problems from Understanding Relativity by Sartori.

Problem 1.3:

A jetliner has an air speed of 500 mph.  A 200 mph wind is blowing from west to east.
(a) The plane heads due north.  What direction does the plane fly and what is its ground speed?
Answer:  First, let us define that the S frame shall be as observed on the ground and the S' frame shall be as observed in the plane.  The magnitude of the plane's velocity with respect to the surrounding air is always 500 mph.  Thus we can say that:

The Galilean transformation from S' to S is:

And the equations of motion in S are:

From this we can say the direction the plane flies in is arc tan (200/500) = 21.8 degrees east of north.  The ground speed is

(b) In what direction should the pilot head in order to fly due north?  What is the plane's ground speed in this case?
Answer:  We are trying to find the angle such that the x component of the velocity in the ground frame is 0.  Using the Galilean transformation, we determine that the x component of velocity in the plane's frame has to be -200 mph, but the magnitude still has to remain 500 mph.  So to get the y component, we need to solve:

The direction the plane flies in is arc tan (200/458.3) = 23.6 degrees west of north and the ground speed is 458.3 mph.

Problem 1.4

A river is 20 m wide; a 1 m/s current flows downstream. Two swimmers, A and B, arrange a race.  A is to swim to a point 20 m downstream and back while B straight across and back.  Each can swim 2 m/s in the water.

(a) in what direction should B head in order to swim straight across.  Illustrate with a sketch.

Answer: In the ground frame S, the total magnitude of B's velocity is 2 m/s.  And we know that the x-direction component is 1 m/s.  Using the Pythagorean theorem, we have:

Taking the arc tan of the two sides, we find that the heading is 30 degrees (π/6 rad) towards the upstream from the straight across position.  Here is the sketch:

(b) Who wins the race and by how much time?

Answer: This question is important since the book takes us through the Michelson-Morley ether detection experiment in the following section.

The speed of B, going straight across and back remains the same the entire time at square root 3 m/s and as such, the elapsed time is 23.09 seconds.

The speed of A changes between the downstream and upstream legs.  For going down stream, she goes at 3 m/s taking 6 2/3 seconds, but going upstream, she goes 1 m/s and takes 20 seconds for a total time of 26.7 seconds.  Thus B wins by about 3 1/2 seconds.

Solving Physics Problems (Part 1)

So I went to Powell's books in downtown Portland and I found a book by Leo Sartori entitled Understanding Relativity: A simplified Approach to Einstein's Theories.  This book deals with Einstein's theory of special relativity.  I've been enthused by the book to try doing the problems at the end of the chapters and I will now share my work with you, dear loyal reader.

Problem 1.1

A train moves at a constant speed.  A stone on the train is released from rest.
(a) using the principle of relativity, describe the motion of the stone as seen by observers on the train.
Answer: As seen by observers on the train, the stone, having the same initial velocity as the train, fall straight down.
(b) Using the Galilean transformation, describe the motion of the stone as seen by observers on the ground.  Draw a sketch.
Answer: To the observer on the ground, the train moves to the right with a speed V.  Therefore, the stone also moves to the right with a speed V as it falls.  See the sketch below:

Problem 1.2

Let V = 30 m/s, h₀ = 7.2 m, approximate g as 10 m/s.

(a) Write the equations that describe the stone's motion in frame S'.

Answer:

S': x' = 0 ; y' = h₀ - ½gt'² ; z' = 0

(b) Use the Galilean transformation to write the equations that describe the position of the stone in frame S.  Plot the curve of the motion of the stone in frame S.

Answer:

The transform from S' → S is as follows:

x = x' + Vt'

y = y'

z = z'

t = t'

The equations of motion in S are:

S: x = Vt ; y = h₀ - ½gt² ; z = 0

Here is the plot of the motion (from Desmos)

(c) Write the equations for the three components of the stone's velocity in S' and use the Galilean transformation to find the component in S.
Answer:
The components of the stone's velocity in S' are:

The Galilean transformation is:

And the components of the stone's velocity in S are:

(d) Find the magnitude of the stone speed in each frame at t = 1 sec.

Answer:

The magnitude of the velocity vector in frame S and S' are:

Solving Math Problems (part 16)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 11

Solve the initial value problem:

xy' = x + y, y(1) = -7.4

Since we solved the general solution in Problem 1 and found it to be y = x( ln |x| + C), we will now simply apply the initial condition.

 -7.4 = 1 ( ln | 1 | + C )

∴ C = -7.4

The specific curve is described by:

y = x ( ln |x| -7.4 )

Section 1.5, Problem 12

Solve the initial value problem:

xy' = 2x +2y, y(0.5) = 0

From here, we find the general solution is:

y = C x² - 2x

Substituting the given initial value, we get:

0 = C (0.25) - 2 (0.5)

∴ C = 4

The specific curve is described by:

y = 4x² - 2x

Section 1.5, Problem 13

Solve the initial value problem:

yy' = x³ + y²/x, y(2) = 6

Dividing by x gives:

(y/x) y' = x² + y²/x²

Changing the variable by u = y/x and y' = u + u'x, we get:

u ( u + u'x ) = x² + u²

Separating the variables and integrating gives:

∫u du = ∫x dx

½u² = ½x² + C

Converting to y gives:

Using the given initial value, we have:

∴ C = 5

The specific solution is

Solving Math Problems (Part 15)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 9

Find the general solution of the following differential equation:

Dividing by x we get:

Changing the variable using u = y/x and y' = u+ u'x, we get:

Simplifying, we get:

Integrating both sides gives:

Changing back to y gives:

Section 1.4, Problem 10

Find the general solution of the following differential equation:

xy' - y -x² tan (y/x) = 0

Dividing by x gives:

y' - (y/x) - x tan (y/x) = 0

Making a change of variable such that u = y/x and y' = u+ u'x, we get:

u + u'x - u - x tan u = 0

Simplifying and separating the variables, we have:

u' cot u = 1

Integrating we get:

ln | sin u | = x + C

Isolating the u gives:

Converting back to y we get:

Solving Math Problems (Part 14)

In doing the problems in section 1.4, I had noticed that a few of the problems seemed to fit a larger classification.  See, for example, problems 1 and 2  In this post, I am going to solve a generalized equation of one sort:

xy' = ax + by

Because there is a point where we divide by b-1, we have to consider two situations.  The simpler is where b = 1.  In this case, we divide everything by x and then use a change of variable where u = y/x and y' = u + u'x.  From this we get:

u + u'x = a + u

u' = a/x

Integrating we get:

u = a ln |x| + C

And converting back to y from u:

y = x (a ln |x| + C )

In the case where b ≠ 1, and using the same change of variable as above, we get:

u + u'x = a + bu

u'x = a + (b-1)u

Integrating both sides, and to be explicit, we will change the variable again by z = a + (b-1)u and dz = (b-1)du to get:

Taking e to the power of both sides, we get:

Taking both sides to the power of (b-1) so as to get z to the first power and then changing back to u, we get:

Rearranged to isolate u, we get:

And converting back to y, we get:

Where c* is defined as:

Summary

Where the differential equation takes the form of

xy' = ax + by

The solution is

Solving Math Problems (Part 13)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 7

Find the general solution of

xy' = y + x² sec (y/x)

Dividing by x gives:

y' = (y/x) + x sec (y/x)

Substituting u = y/x and y' = u + u'x we get:

u + u'x = u + x sec u

Re-arranging we get:

∫cos u du = ∫ dx

sin u = x + C

u = arc sin (x + C)

y = x arc sin (x + C)

Section 1.4, Problem 8

Find the general solution of

Substituting u = y/x and y' = u + u'x we get:

u(u + u'x) = u² + x/(x²+1)

Simplifying we get:

uu' = 1/(x² + 1)

Integrating both sides, we have:

u²/2 = arc tan x + C

Substituting y = ux, we have:

Solving Math Problems (Part 12)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 5

Find the general solution of:

x²y' = x² - xy + y²

Dividing by x² we get

Changing the variable using u = y/x and y' = u + u'x we get

u + u'x = 1 - u + u²

Rearranging we get:

Integrating both sides:



Substituting back y instead of u, we have:

Section 1.4, Problem 6

Find the general solution of:

xy' - y = 3x⁴cos²( y / x )

Rearranging we get:

y' - (y/x) = 3x³ cos²( y / x )

Changing the variable using u = y/x and y' = u + u'x we get

u + u'x - u = 3x³ cos² u

Separating the variables we have:

Integrating both sides we have:

tan u = x³ + C

u = arc tan (x³ + C)

Changing back to y gives:

y = x arc tan (x³ + C)

Solving Math Problems (Part 11)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, problem 3

Find the general solution to:

xy' = (y - x)³ + y

Expanding the bracket and dividing everything by x³ we get:

Using a change of variable where u = y/x and y' = u + u'x we get:

Simplifying we get:

Separating the variables by cross multiplication and then integrating both sides we have:

Some re-arrangement is necessary before we can convert back to y from u.

Converting back to y from u we have:

Section 1.4, Problem 4

Find the general solution of:

xy' = y² + y

Dividing by x² we get:

Change of variable using u = y/x and y' = u + u'x gives:

This simplifies to:

u' = u²

Integrating, we get:

 Re-arranging:

 Changing back to y from u gives