Section 1.4, Problem 7
Find the general solution of
xy' = y + x² sec (y/x)
Dividing by x gives:
y' = (y/x) + x sec (y/x)
Substituting u = y/x and y' = u + u'x we get:
u + u'x = u + x sec u
Re-arranging we get:
∫cos u du = ∫ dx
sin u = x + C
u = arc sin (x + C)
y = x arc sin (x + C)
Section 1.4, Problem 8
Find the general solution ofSubstituting u = y/x and y' = u + u'x we get:
u(u + u'x) = u² + x/(x²+1)
Simplifying we get:
uu' = 1/(x² + 1)
Integrating both sides, we have:
u²/2 = arc tan x + C
Substituting y = ux, we have:


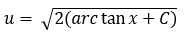

No comments:
Post a Comment