More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.
Section 1.4, Problem 5
Find the general solution of:
x²y' = x² - xy + y²
Dividing by x² we getChanging the variable using u = y/x and y' = u + u'x we get
u + u'x = 1 - u + u²
Rearranging we get:
Integrating both sides:
Substituting back y instead of u, we have:
Section 1.4, Problem 6
Find the general solution of:
xy' - y = 3x⁴cos²( y / x )
Rearranging we get:
y' - (y/x) = 3x³ cos²( y / x )
Changing the variable using u = y/x and y' = u + u'x we get
u + u'x - u = 3x³ cos² u
Separating the variables we have:Integrating both sides we have:
tan u = x³ + C
u = arc tan (x³ + C)
Changing back to y gives:
y = x arc tan (x³ + C)




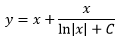

No comments:
Post a Comment