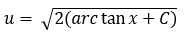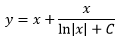About "random" numbers

It is an interesting thing that if you were to ask some person to give you a "random" 6-digit number, they would tend to try really hard to not repeat digits.  People have a tendency to think that random number do not have repeating digits.  But an analysis of these numbers shows that, in fact, for longer numbers, it starts to be more likely that there are repeated digits than not.  Below is a table of the number of digits and the likelihood that there are repeating digits.
(argh, excuse me but there is not a control to create a table!!)
Number of digits vs. likelihood of repeated digits:

1. None
2. 9.99%
3. 28%
4. 50%
5. 70%
6. 85%
7. 94%
8. 98%
9. 99%
10. nearly 100%

So the psychology going on here is that people have a sense in 2 digit and maybe 3 digit numbers that repeated digits in a number are rarer than unique.  However, in reality, when you get to 5 and 6 digit numbers, most numbers have repeated digits.
The math of permutations and combinations is explained here .
The python math module functions are explained here.  The ones that are relevant are the factorial, comb and perm functions.  I wrote some code to re-create these.  I found out that after 10 levels of recursion, Python gives you an error message.  So I had to use the math module version of the factorial function.

# This defines the permutation function

# and the combination function

from math import factorial

def perm(n,r):

    return factorial(n)/factorial(n-r)

def comb(n,r):

    return factorial(n)/factorial(n-r)/factorial(r)

for i in range(2,11):

    print(i,1-perm(10,i)/10**i)

Also, if you don't believe the math, I also wrote a piece of code that does a brute force calculation.  It does take some time to work its way through all the different combinations.  And it will not give the exact same results since it is not considering the numbers that start with 0.

 

# This program prints out how many of the numbers in a range

# have repeating digits

n = 2

flag = True

while flag:

    test = 10**(n-1)

    count = 0

    print(test)

    while test < 10**n:

        a = str(test)

        dupe = False

        for i in range(10):

            if a.count(str(i))>1:

                dupe = True

        if dupe:

            count = count + 1

        test = test +1

    ratio = count / 10**n

    print(n,count, ratio)

    ask = input("continue? (n to end) >")

    if ask == 'n':

        flag = False

    n = n+1

So it's an interesting bit of psychology so I hope you enjoy it.             

Solving Math Problems (Part 17)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 14

Solve the following initial value problem:

xyy' = 2y² + 4 x², y(2) = 4

Dividng by x² we get:

(y/x) y' = 2(y/x)² + 4

Changing the variable u = y/x, y' = u + u'x we get:

u(u + u'x) = 2u² + 4

u² + uu'x = 2u² + 4

uu' / (u² + 4) = 1 / x

Integrating both sides we get:

We now make another change of variable to z such that z = u² + 4 and dz = 2u du.

½ln |z| = ln |x| + C

Changing back to u from z gives

½ln |u² + 4| = ln |x| + C

Taking e to the power of both sides gives:

Re-arranging to isolate u gives:

And finally changing back to y from u we have:

Now using the initial condition, we find that C = 2 and thus the specific function that satisfies the differential equation with this initial condition is:

Section 1.4, Problem 15

Find the function that satisfies:

Rearranging we get:

yy' - xy' = y + x

Dividing by x gives:

(y/x) y' - y' = (y/x) + 1

Now changing variable with u = (y/x) and y' = u + u'x

u (u + u'x) - (u + u'x) = u + 1

u² + uu'x - u - u'x = u + 1

uu'x - u'x = 1 + 2u - u²

u'x(u - 1) = 1 + 2u - u²

We make another change of variable such that z = 1 + 2u - u² and dz = (2 - 2u) du and we get:

Integrating both sides gives:



½ln|z| = ln|x| + C

z = Cx²

Changing back to u from z:

1 + 2u - u² = Cx²

Changing back to y from u:

x² + 2xy - y² = C

Then using the initial condition, we find that C = -4

Solving Math Problems (part 16)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 11

Solve the initial value problem:

xy' = x + y, y(1) = -7.4

Since we solved the general solution in Problem 1 and found it to be y = x( ln |x| + C), we will now simply apply the initial condition.

 -7.4 = 1 ( ln | 1 | + C )

∴ C = -7.4

The specific curve is described by:

y = x ( ln |x| -7.4 )

Section 1.5, Problem 12

Solve the initial value problem:

xy' = 2x +2y, y(0.5) = 0

From here, we find the general solution is:

y = C x² - 2x

Substituting the given initial value, we get:

0 = C (0.25) - 2 (0.5)

∴ C = 4

The specific curve is described by:

y = 4x² - 2x

Section 1.5, Problem 13

Solve the initial value problem:

yy' = x³ + y²/x, y(2) = 6

Dividing by x gives:

(y/x) y' = x² + y²/x²

Changing the variable by u = y/x and y' = u + u'x, we get:

u ( u + u'x ) = x² + u²

Separating the variables and integrating gives:

∫u du = ∫x dx

½u² = ½x² + C

Converting to y gives:

Using the given initial value, we have:

∴ C = 5

The specific solution is

Solving Math Problems (Part 15)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 9

Find the general solution of the following differential equation:

Dividing by x we get:

Changing the variable using u = y/x and y' = u+ u'x, we get:

Simplifying, we get:

Integrating both sides gives:

Changing back to y gives:

Section 1.4, Problem 10

Find the general solution of the following differential equation:

xy' - y -x² tan (y/x) = 0

Dividing by x gives:

y' - (y/x) - x tan (y/x) = 0

Making a change of variable such that u = y/x and y' = u+ u'x, we get:

u + u'x - u - x tan u = 0

Simplifying and separating the variables, we have:

u' cot u = 1

Integrating we get:

ln | sin u | = x + C

Isolating the u gives:

Converting back to y we get:

Solving Math Problems (Part 14)

In doing the problems in section 1.4, I had noticed that a few of the problems seemed to fit a larger classification.  See, for example, problems 1 and 2  In this post, I am going to solve a generalized equation of one sort:

xy' = ax + by

Because there is a point where we divide by b-1, we have to consider two situations.  The simpler is where b = 1.  In this case, we divide everything by x and then use a change of variable where u = y/x and y' = u + u'x.  From this we get:

u + u'x = a + u

u' = a/x

Integrating we get:

u = a ln |x| + C

And converting back to y from u:

y = x (a ln |x| + C )

In the case where b ≠ 1, and using the same change of variable as above, we get:

u + u'x = a + bu

u'x = a + (b-1)u

Integrating both sides, and to be explicit, we will change the variable again by z = a + (b-1)u and dz = (b-1)du to get:

Taking e to the power of both sides, we get:

Taking both sides to the power of (b-1) so as to get z to the first power and then changing back to u, we get:

Rearranged to isolate u, we get:

And converting back to y, we get:

Where c* is defined as:

Summary

Where the differential equation takes the form of

xy' = ax + by

The solution is

Solving Math Problems (Part 13)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 7

Find the general solution of

xy' = y + x² sec (y/x)

Dividing by x gives:

y' = (y/x) + x sec (y/x)

Substituting u = y/x and y' = u + u'x we get:

u + u'x = u + x sec u

Re-arranging we get:

∫cos u du = ∫ dx

sin u = x + C

u = arc sin (x + C)

y = x arc sin (x + C)

Section 1.4, Problem 8

Find the general solution of

Substituting u = y/x and y' = u + u'x we get:

u(u + u'x) = u² + x/(x²+1)

Simplifying we get:

uu' = 1/(x² + 1)

Integrating both sides, we have:

u²/2 = arc tan x + C

Substituting y = ux, we have:

Solving Math Problems (Part 12)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, Problem 5

Find the general solution of:

x²y' = x² - xy + y²

Dividing by x² we get

Changing the variable using u = y/x and y' = u + u'x we get

u + u'x = 1 - u + u²

Rearranging we get:

Integrating both sides:



Substituting back y instead of u, we have:

Section 1.4, Problem 6

Find the general solution of:

xy' - y = 3x⁴cos²( y / x )

Rearranging we get:

y' - (y/x) = 3x³ cos²( y / x )

Changing the variable using u = y/x and y' = u + u'x we get

u + u'x - u = 3x³ cos² u

Separating the variables we have:

Integrating both sides we have:

tan u = x³ + C

u = arc tan (x³ + C)

Changing back to y gives:

y = x arc tan (x³ + C)

Solving Math Problems (Part 11)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.4, problem 3

Find the general solution to:

xy' = (y - x)³ + y

Expanding the bracket and dividing everything by x³ we get:

Using a change of variable where u = y/x and y' = u + u'x we get:

Simplifying we get:

Separating the variables by cross multiplication and then integrating both sides we have:

Some re-arrangement is necessary before we can convert back to y from u.

Converting back to y from u we have:

Section 1.4, Problem 4

Find the general solution of:

xy' = y² + y

Dividing by x² we get:

Change of variable using u = y/x and y' = u + u'x gives:

This simplifies to:

u' = u²

Integrating, we get:

 Re-arranging:

 Changing back to y from u gives