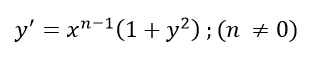Solving Math Problems (Part 6)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.2, Problem 18

Solve

y' + csc y = 0

Separating the variable we get:

y' sin y = -1

Integrating both sides we get:

∫ sin y dy = -∫ dx

- cos y = -x + C

Multiplying by -1 and taking the arc cos of both sides gives:

y = arc cos (x + C)

Section 1.2, Problem 19

Solve the initial value problem:

xy' + y = 0 given y(1) = 1

Separating the variables gives:

Integrating both sides gives:

ln | y | = - ln | x | + C

Applying the initial condition of y(1) = 1, solves C = 1 and the solution is y = 1 / x.

Section 1.2, Problem 20

Solve the initial value problem:

y' = - x / y given y(2) = ⎷5

Separating the variables we get:

y y'  = - x

Integrating both sides we have:

∫ y dy = - ∫ x dx

½ y² = - ½ x² + C

Using the initial condition, solving for C we get C = 4.5 so that the solution is:

Solving Math Problems (Part 5)

More problems from Advanced Engineering Mathematics, 6th Edition by Kreyszig.

Section 1.2, Problem 15

Solve

(x ln x) y' = y

Separating the variables gives:

Integrating both sides gives:

For the right hand side, we perform a change of variable with u = ln x, du = dx / x and get:

ln | y | = ln | u | + C

Substitution ln x for u gives:

ln | y | = ln | ln | x | | + C

Taking e to the power of both sides gives:

y = C ln | x |

Section 1.2, Problem 16

Solve

Separating the variables gives

Integrating both sides gives:

Section 1.2, Problem 17

Solve

y' sin 2x = y cos 2x

Separating the variables gives:

Integrating both sides gives:

ln | y | = ln | sin 2x | + C

Taking e to the power of both sides gives

y = C sin 2x

Solving Math Problems (part 4)

Here are the next problems in Erwin Kreyszig's Advanced Engineering Mathematics, 6th edition.

Section 1.2, Problem 12

Solve the differential equation

Separating variables gives:

Integrating both sides gives:

The left-hand side is solved from the table of integrals in the front cover of the textbook.

arc tan y = 𝜋 x + C

y = tan ( 𝜋 x + C)

Section 1.2, Problem 13

Solve the differential equation

Separating variables gives:

Integrating both sides gives:

The left hand side is solved using an identity from the front cover of the text book.

arc sin y = x + C

y = sin (x + C)

Section 1.2, Problem 14

Solve the differential equation

y' + y² = 1

Separating the variables gives:

Integrating both sides gives:

The left hand side looks like it should be a trig identity, but it is not, it is solved via trigonometric substitution, but using Jan J. Tuma's Engineering Mathematics Handbook, 3rd Edition, Section 19, table 10 tells us that the solution to the left hand side is:

This can be manipulated over several steps to result in:



Solving Math Problems (Part 3)

These are math problems presented in Erwin Kreyszig's Advanced Engineering Mathematics, 6th Edition.  We have been working on the problems at the end of section 1.2

Section 1.2, Problem 10

Solve

(y - b) y' = a - x

Since the variables are already separated, we can proceed immediately to integrate both sides:

This is basically the equation for a circle centered at (a,b).  Some algebraic manipulation (multiply through by 2, moving everything over to one side, complete the squares by adding a²+b² and further rearrangement gets you to a standard circle equation.

(x - a)² + (y - b)² = R² = 2C + a² + b²

Section 1.2, Problem 11

Solve

Separating the variables we get:

Integrating both sides:

Rearranging gives the seemingly impossible:

So I had to run this graph in Desmos and see what it looked like.

The equation creates graphs only when C < 0.  For values C ≥ 0, the function produces complex numbers.

Solving Math problems part 2

Here are more problems solved from section 1.2 in Advanced Engineering Mathematics, 6th edition by Erwin Kreyszig.  Up to taking this Differential Equations math course, I had found everything else in math to be intuitive.  This course started off that way, but later I had to work to understand the concepts.

Section 1.2, Problem 6

Solve

xy' = 5y

Rearranging we have:

Integrating we get:

ln |y| = ln |5x| + C

y = 5Cx

Section 1.2, Problem 7

Solve

y’ = 3x²y

Re-arranging we have:

y'/y = 3x²

Integrating we get:

ln |y| = x³ + C

Section 1.2, Problem 8

Solve

xy' = ny

We note that this is a general case of problem 6 where for 6, n = 5.  As such, we conclude that the solution is

y=nCx

Section 1.2, Problem 9

Solve

y' + ay + b = 0 (a ≠ 0)

By moving the ay+b to the other size and then dividing we get:

Integrating we get:

The left-hand side can be solve by u substitution where u = ay +b and du = ady, but I will use a table of integrals, specifically table (4) of section 19 from Engineering Mathematics Handbook, 3rd Edition, by Jan J. Tuma.  Solving the integrals we get:

Multiplying both sides by b and then taking e to the power of both sides, we get:

Finally, some rearrangement gives us the answer:

Solving math problems

Searching around for something that is interesting to write about and for which there even might be an audience, I've decided I am going to do math problems out of my last university math text book, that being the one I used for a Differential Equations course, Advanced Engineering Mathematics, 6th Edition by Erwin Kreyszig.

Section 1.2, Problem 3

Solve

y'=ky.

Rearranging we get:

y'/y=k

Integrating we have:

∫dy/y = ∫kdx

ln y = kx + C

Section 1.2, Problem 4

Solve

y' = sec y

Rearranging we get:

y' cos y = 1

Integrating we have:

sin y = x + C

y = arc sin x + C

Section 1.2, Problem 5

Solve

y' = y cot x

Rearranging we get:

Integrating we have:

ln |y| = ln |sin x| + C

y = C |sin x|

How to deal with existential threats

I have been recently listening to an audiobook version of Steven Pinker's Enlightenment Now.  As a result I have been thinking about what are the real risks of existential threats to humanity as well as the liberal western secular democracies which seem to be at the pinnacle of human achievement currently.  The point of this is to put together some thoughts on what can actually be done to mitigate the risks of existential threats.  First, I want to go through a number of these threats to try and define characteristics of the threats, create some kind of categorization and finally give some thoughts to how to proceed to combat those characteristics.

Conspiracy theories

In looking at ways that humanity could be wiped off the face of the Earth or at least reduced technologically to some primitive hunter-gatherer or simple agricultural state, there are many possible mechanisms that have been proposed to do this.  I will give a brief synopsis of a dozen or so in no particular order

Gray goo

The goo can vary between genetically engineered bacteria to nanobots to even some kind of hypothetical alien being or technology that is introduced via space travel or comet (spaceship?) impact with the Earth.  In any case, there is something that simply converts whatever it touches into goo, removing the life and organization from the matter, destroying everything it comes in contact with.  A nice fictionalized version of this is Vonnegut's Cat's Cradle with the substance Ice Nine.

It came from space

There have been asteroid and comet impacts before and doubtlessly again in the future.  Comet impacts, but also other spatial hazards such as the sun going out, radiation, etc. fall into this category including missiles launched by hypothetical aliens.  Another space type hazard is the scenario where a particle accelerator creates a black hole and it then pulls in the entirety of the planet, the moon and eventually the entire sun.

Conquest

Some external force takes over from humans and in the process makes us go extinct.  Some possible sources are apes, high mortality infectious disease or hypothetical aliens or even zombies.

Changes to the environment

This includes all kinds of changes to the environment so that it is too hot, too cold, too dry, too acidic, too basic, too salty, too much radiation to sustain life anymore.  There are all kinds of reasons why there could be changes, some related to human activity, and others not.

Classification of the threat

I would propose classifying the threats on a few scales.  The first is the speed of arrival.  Since nothing can move faster than the speed of light, that would be the top of the scale.  Some of the astronomical or physics based existential threats do move at the speed of light.  But many threats are slower such as the sun going out.
The second scale would be the extent of human control there is on the threat.  Some threats such as asteroids and comets are outside our control.  Other threats such as nuclear war definitely are.
A third scale would be how between when it starts and annihilation.  For example, a supernova (not that our sun would ever supernova as it is too small) is over very quickly, but infectious disease might take a decade before it manages to kill everyone.
The kinds of existential threats that are easiest to handle are those that are entirely within our control, arrive slowly (can be seen years ahead) and take time to happen (allows for reaction).  We need to try and work towards shifting these scales for all threats in those directions, if possible.  For example, better detection of asteroids and comets, better control of research into new infectious diseases.  Our best tools to do this are evidence based science.